|
力扣算法(LeetCode)第224题是一道对编程新手比较友好的题:制作一个简单的加减计算器,计算只有加减没有乘除,并且要求带括号。 比如像下面这个计算式:12-(34+56)+78-90 计算它的结果。
计算效果展示这个计算式看着简单,似乎是小学水平的题,但力扣官方给它的难度定位是“困难”,我试着自己用C++做了一下,确实非常困难、没有思路。 本题难点主要是那个圆括号比较复杂,圆括号里的计算式要优先计算,并且受到圆括号前的加减符号控制。这个知识点,对于人类来说好理解,但是,要让计算机理解就有难度了,我虽然想到了用堆栈方式处理,但是在编程时,这个思路不太好落地,并不太容易用简单方法处理。 于是我直接参考官方答案的思路(我自己的大脑想不出来):利用栈(Stack)的功能,做一个记号(sign)控制数字前的计算符号。计算逻辑还是有一定难度的。
力扣算法224题的算法原理分步骤展示力扣这道题下面的评论说:字节跳动面试很爱考这道题。不过我选这道题重点讲解的原因不是因为这个,而是因为这种计算加减乘除的题目更具体、更贴近日常生活、容易理解、也更有乐趣。本文讲解力扣224题解题思路分为以下4个部分:1.题目描述;2.官方题解;3.官方题解原理演示;4.算法总结。 1.题目描述力扣224题的题干部分是这样的:给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
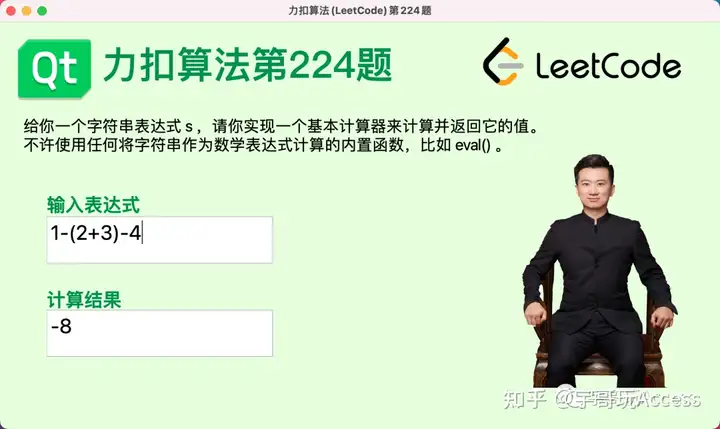
我用Qt做出的本题(简单计算器)界面(苹果电脑版)示例 1:输入:s = "1+1"输出:2 示例 2:输入:s = "2-1+2 "输出:3 示例 3:输入:s = "(1+(4+5+2)-3)+(6+8)"输出:23 2.官方题解官方答案给的完整代码如下,可以直接在Qt里调用: - class Solution
- {
- public:
- int calculate(std::string s)
- /*声明一个名为Solution的类,该类包含一个名为calculate的方法,
- 该方法接受一个字符串s作为输入,并返回一个整数。*/
- {
- std::stack<int> ops;//建立一个堆栈stack
- ops.push(1);
- int sign = 1;
- /*声明一个名为ops的堆栈stack,用于记录每个操作数的符号。
- 将初始值为1的符号压入堆栈中。定义一个名为sign的整型变量,
- 用于表示当前操作数的符号,并将其初始化为1。*/
- int result = 0;
- int n = s.length();
- int i = 0;
- /*定义一个名为ret的整型变量,用于记录计算结果,并将其初始化为0。
- 定义一个名为n的整型变量,用于表示输入字符串的长度。
- 定义一个名为i的整型变量,用于表示当前处理到输入字符串的哪个位置。*/
- while (i < n)//开始一个while循环,当i小于输入字符串的长度时执行。
- {
- if (s[i] == ' ')
- {
- i++;//如果当前字符是空格,则将i加1,跳过该字符。
- }
- else if (s[i] == '+')
- {
- sign = ops.top();
- i++;//如果当前字符是加号,则将当前符号sign设置为堆栈顶部的符号,然后将i加1。
- }
- //如果当前字符是减号,则将当前符号sign设置为堆栈顶部的符号的相反数,然后将i加1。
- else if (s[i] == '-')
- {
- sign = -ops.top();
- i++;
- }
- else if (s[i] == '(')//如果当前字符是左括号,则将当前符号sign压入堆栈中,然后将i加1。
- {
- ops.push(sign);
- i++;
- }
- else if (s[i] == ')')//如果当前字符是右括号,则从堆栈中弹出一个符号,然后将i加1。
- {
- ops.pop();
- i++;
- }
- /*如果当前字符是数字,则从字符串中提取该数字,将其与当前符号相乘,然后将结果加到计算结果ret中。
- 具体来说,通过一个while循环从字符串中提取数字num,并将其累加到变量num中,直到遇到非数字字符。
- 然后将sign乘以num,得到当前操作数的实际值,将其加到计算结果ret中。
- 最后,将i加1,继续处理下一个字符。*/
- else
- {
- long num = 0;
- while (i < n && s[i] >= '0' && s[i] <= '9')
- {
- num = num * 10 + s[i] - '0';
- i++;
- }
- result += sign * num;
- }
- }
- return result;//返回计算结果ret作为方法的输出,并结束方法和类的定义。
- }
- };
3.官方题解原理演示官方代码写得非常精炼,对于编程老手来说不难理解。但是对于初学入门者来说就并不容易理解了。虽然官方每一行代码,我都尽可能的用人类语言来解释是做什么用的,但是还是很难读懂。因此进行原理过程的逐步演示非常必要。这道题的原理是把输入的计算式“1-(2+3)-4”重头到尾遍历一遍,遇见什么符号就相应的进行处理,一边遍历一边进行求和计算。 我们以一个非常简单的计算式“1-(2+3)-4”来进行逐步骤的演示,有助于大家的理解。 遍历前的准备: 这个计算式“1-(2+3)-4”中一共有9个元素:4个数字、3个计算符号和2个括号。我们按照力扣官方答案给的代码,从左到右开始遍历这9个元素,看看会发生什么。 在正式遍历之前,系统先自动准备一个栈stack。  在正式循环前,先把sign设置成1,然后把1这个常量推进栈里。 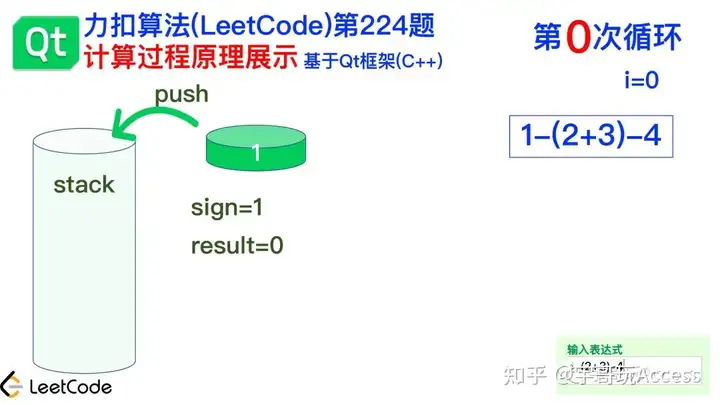 遍历第1个元素为“1”,根据程序设定进行了直接计算(根据程序设定,只有在遍历为数字的时候才进行计算)。 - else
- {
- long num = 0;
- while (i < n && s[i] >= '0' && s[i] <= '9')
- {
- num = num * 10 + s[i] - '0';
- i++;
- }
- result += sign * num;
- }
计算式为sign*num=1*1=1  遍历第2个符号为“-”,根据程序设定,sign值变成栈顶元素的相反数,计算式不进行计算。 - else if (s[i] == '-')
- {
- sign = -ops.top();
- i++;
- }
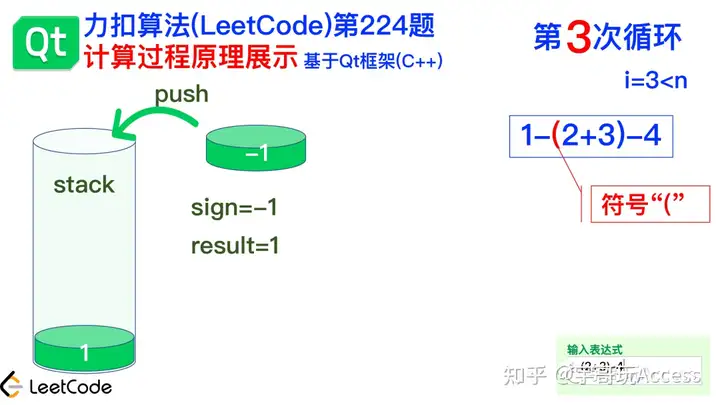
因此sign变成-1。  遍历到第3个符号“(”,根据程序设定,将sigh=-1推入栈中,因此目前的栈顶元素是-1。 - else if (s[i] == '(')//如果当前字符是左括号,则将当前符号sign压入堆栈中,然后将i加1。
- {
- ops.push(sign);
- i++;
- }
 遍历第4个符号为数字,进行求和计算,注意是累加计算,也就是上一个数字计算的结果再加上本次计算的结果:1+2*(-1)=-1  遍历第5个符号是“+”。根据程序安排,sign取值为栈顶元素,其他不变。 - else if (s[i] == '+')
- {
- sign = ops.top();
- i++;//如果当前字符是加号,则将当前符号sign设置为堆栈顶部的符号,然后将i加1。
- }
 遍历第6个符号为数字,进行求和计算,注意是累加计算,也就是上一个数字计算的结果再加上本次计算的结果:-1+3*(-1)=-4。  遍历到第7个符号“)”,根据程序设定,将栈顶元素-1推出栈外,因此目前的栈顶元素是1。 - else if (s[i] == ')')//如果当前字符是右括号,则从堆栈中弹出一个符号,然后将i加1。
- {
- ops.pop();
- i++;
- }
 遍历第8个符号为“-”,根据程序设定,sign值变成栈顶元素的相反数,计算式不进行计算。也就是sign=-1。  遍历第9个符号为数字,进行求和计算,注意是累加计算,也就是上一个数字计算的结果再加上本次计算的结果:-4+4*(-1)=-9  遍历完第9个元素之后,i>n=9,循环结束,最终答案就是-8。 4.算法总结本案例非常的直观,用了一个栈来专门处理指示符号sign,处理计算式里的括号,很巧妙。案例这个计算式“1-(2+3)-4”中一共有9个元素:4个数字、3个计算符号和2个括号,数字、加减号和括号分别用不同方法处理: (1)数字就进行累计计算,sign乘以数字加上上次数字计算的结果; (2)计算符号进行sign赋值计算,加号sign就是+1,减号sign就是-1 (3)括号是个难点,左括号"("就进行入栈操作push,把sign数字推入栈中,右括号")"就进行出站操作pop,把栈顶数字推出。 官方答案看似简单,但是逻辑还真不简单,想要吃透这个算法,最好自己分步骤推导一下。
|  |小黑屋|宇哥编程论坛
( 京ICP备2022024677号-2|
|小黑屋|宇哥编程论坛
( 京ICP备2022024677号-2|![]() 京公网安备11011202100561号 )
京公网安备11011202100561号 )